Symbolic Regression¤
This example combines neural differential equations with regularised evolution to discover the equations
\(\frac{\mathrm{d} x}{\mathrm{d} t}(t) = \frac{y(t)}{1 + y(t)}\)
\(\frac{\mathrm{d} y}{\mathrm{d} t}(t) = \frac{-x(t)}{1 + x(t)}\)
directly from data.
References:
This example appears as an example in Section 6.1 of:
@phdthesis{kidger2021on,
title={{O}n {N}eural {D}ifferential {E}quations},
author={Patrick Kidger},
year={2021},
school={University of Oxford},
}
Whilst drawing heavy inspiration from:
@inproceedings{cranmer2020discovering,
title={{D}iscovering {S}ymbolic {M}odels from {D}eep {L}earning with {I}nductive
{B}iases},
author={Cranmer, Miles and Sanchez Gonzalez, Alvaro and Battaglia, Peter and
Xu, Rui and Cranmer, Kyle and Spergel, David and Ho, Shirley},
booktitle={Advances in Neural Information Processing Systems},
publisher={Curran Associates, Inc.},
year={2020},
}
@software{cranmer2020pysr,
title={PySR: Fast \& Parallelized Symbolic Regression in Python/Julia},
author={Miles Cranmer},
publisher={Zenodo},
url={http://doi.org/10.5281/zenodo.4041459},
year={2020},
}
This example is available as a Jupyter notebook here.
import tempfile
import equinox as eqx # https://github.com/patrick-kidger/equinox
import jax
import jax.numpy as jnp
import optax # https://github.com/deepmind/optax
import pysr # https://github.com/MilesCranmer/PySR
import sympy
import sympy2jax # https://github.com/google/sympy2jax
Now two helpers. We'll use these in a moment; skip over them for now.
class Stack(eqx.Module):
modules: list[eqx.Module]
def __call__(self, x):
assert x.shape[-1] == 2
x0 = x[..., 0]
x1 = x[..., 1]
return jnp.stack([module(x0=x0, x1=x1) for module in self.modules], axis=-1)
def quantise(expr, quantise_to):
if isinstance(expr, sympy.Float):
return expr.func(round(float(expr) / quantise_to) * quantise_to)
elif isinstance(expr, (sympy.Symbol, sympy.Integer)):
return expr
else:
return expr.func(*[quantise(arg, quantise_to) for arg in expr.args])
Okay, let's get started.
We start by running the Neural ODE example. Then we extract the learnt neural vector field, and symbolically regress across this. Finally we fine-tune the resulting symbolic expression.
def main(
symbolic_dataset_size=2000,
symbolic_num_populations=100,
symbolic_population_size=20,
symbolic_migration_steps=4,
symbolic_mutation_steps=30,
symbolic_descent_steps=50,
pareto_coefficient=2,
fine_tuning_steps=500,
fine_tuning_lr=3e-3,
quantise_to=0.01,
):
#
# First obtain a neural approximation to the dynamics.
# We begin by running the previous example.
#
# Runs the Neural ODE example.
# This defines the variables `ts`, `ys`, `model`.
print("Training neural differential equation.")
%run neural_ode.ipynb
#
# Now symbolically regress across the learnt vector field, to obtain a Pareto
# frontier of symbolic equations, that trades loss against complexity of the
# equation. Select the "best" from this frontier.
#
print("Symbolically regressing across the vector field.")
vector_field = model.func.mlp # noqa: F821
dataset_size, length_size, data_size = ys.shape # noqa: F821
in_ = ys.reshape(dataset_size * length_size, data_size) # noqa: F821
in_ = in_[:symbolic_dataset_size]
out = jax.vmap(vector_field)(in_)
with tempfile.TemporaryDirectory() as tempdir:
symbolic_regressor = pysr.PySRRegressor(
niterations=symbolic_migration_steps,
ncycles_per_iteration=symbolic_mutation_steps,
populations=symbolic_num_populations,
population_size=symbolic_population_size,
optimizer_iterations=symbolic_descent_steps,
optimizer_nrestarts=1,
procs=1,
model_selection="score",
progress=False,
tempdir=tempdir,
temp_equation_file=True,
)
symbolic_regressor.fit(in_, out)
best_expressions = [b.sympy_format for b in symbolic_regressor.get_best()]
#
# Now the constants in this expression have been optimised for regressing across
# the neural vector field. This was good enough to obtain the symbolic expression,
# but won't quite be perfect -- some of the constants will be slightly off.
#
# To fix this we now plug our symbolic function back into the original dataset
# and apply gradient descent.
#
print("\nOptimising symbolic expression.")
symbolic_fn = Stack([sympy2jax.SymbolicModule(expr) for expr in best_expressions])
symbolic_model = eqx.tree_at(lambda m: m.func.mlp, model, symbolic_fn) # noqa: F821
@eqx.filter_grad
def grad_loss(symbolic_model):
vmap_model = jax.vmap(symbolic_model, in_axes=(None, 0))
pred_ys = vmap_model(ts, ys[:, 0]) # noqa: F821
return jnp.mean((ys - pred_ys) ** 2) # noqa: F821
optim = optax.adam(fine_tuning_lr)
opt_state = optim.init(eqx.filter(symbolic_model, eqx.is_inexact_array))
@eqx.filter_jit
def make_step(symbolic_model, opt_state):
grads = grad_loss(symbolic_model)
updates, opt_state = optim.update(grads, opt_state)
symbolic_model = eqx.apply_updates(symbolic_model, updates)
return symbolic_model, opt_state
for _ in range(fine_tuning_steps):
symbolic_model, opt_state = make_step(symbolic_model, opt_state)
#
# Finally we round each constant to the nearest multiple of `quantise_to`.
#
trained_expressions = []
for symbolic_module in symbolic_model.func.mlp.modules:
expression = symbolic_module.sympy()
expression = quantise(expression, quantise_to)
trained_expressions.append(expression)
print(f"Expressions found: {trained_expressions}")
main()
Training neural differential equation.
Step: 0, Loss: 0.16657482087612152, Computation time: 11.210124731063843
Step: 100, Loss: 0.01115578692406416, Computation time: 0.002620220184326172
Step: 200, Loss: 0.006481764372438192, Computation time: 0.0026247501373291016
Step: 300, Loss: 0.0013819701271131635, Computation time: 0.003179311752319336
Step: 400, Loss: 0.0010746140033006668, Computation time: 0.0031697750091552734
Step: 499, Loss: 0.0007994902553036809, Computation time: 0.0031609535217285156
Step: 0, Loss: 0.028307927772402763, Computation time: 11.210363626480103
Step: 100, Loss: 0.005411561578512192, Computation time: 0.020294666290283203
Step: 200, Loss: 0.004366496577858925, Computation time: 0.022084712982177734
Step: 300, Loss: 0.0018046485492959619, Computation time: 0.022309064865112305
Step: 400, Loss: 0.001767474808730185, Computation time: 0.021766185760498047
Step: 499, Loss: 0.0011962582357227802, Computation time: 0.022264480590820312
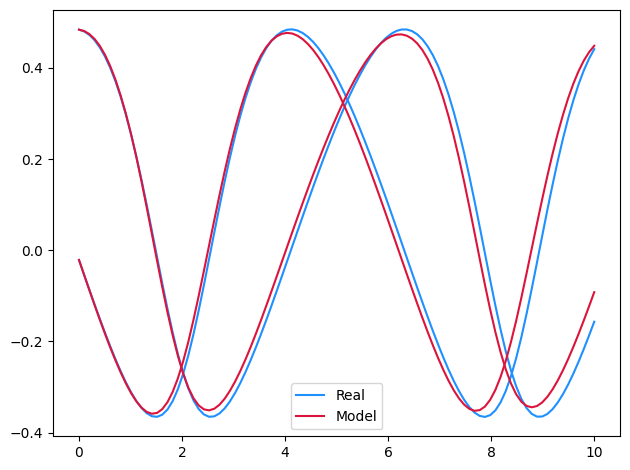
Symbolically regressing across the vector field.
Started!
Cycles per second: 5.190e+03
Head worker occupation: 3.3%
Progress: 434 / 800 total iterations (54.250%)
==============================
Best equations for output 1
Hall of Fame:
-----------------------------------------
Complexity Loss Score Equation
1 4.883e-02 1.206e+00 x1
3 2.746e-02 2.877e-01 (x1 + -0.14616892)
5 6.162e-04 1.899e+00 (x1 / (x1 - -1.0118991))
7 4.476e-04 1.598e-01 ((x1 / 0.92953163) / (x1 + 1.0533974))
9 3.997e-04 5.664e-02 (((x1 * 1.0935224) + -0.008988203) / (x1 + 1.0716586))
13 3.364e-04 4.306e-02 (x1 * ((((x0 * -0.94923264) / 11.808947) - -1.087501) / (x1 + 1.0548282)))
15 3.062e-04 4.714e-02 (x1 * ((((x0 * (-1.1005011 - x1)) / 13.075972) - -1.0955853) / (x1 + 1.0604433)))
==============================
Best equations for output 2
Hall of Fame:
-----------------------------------------
Complexity Loss Score Equation
1 1.588e-01 -1.000e-10 -0.002322703
3 2.034e-02 1.028e+00 (0.14746223 - x0)
5 1.413e-03 1.333e+00 (x0 / (-1.046938 - x0))
7 6.958e-04 3.543e-01 (x0 / ((x0 + 1.1405994) / -1.1647526))
9 2.163e-04 5.841e-01 (((x0 + -0.026584703) / (x0 + 1.2191753)) * -1.2456053)
11 2.163e-04 7.749e-06 ((x0 - 0.026545616) / (((x0 / -1.2450436) + -0.9980602) - -0.019172505))
==============================
Press 'q' and then <enter> to stop execution early.
Optimising symbolic expression.
Expressions found: [x1/(x1 + 1.0), x0/(-x0 - 1.0)]